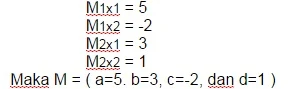Metode Pembelajaran Tentang Dasar Matriks
Halo sahabat MB dimana pun anda berada, di bawah ini saya akan memaparkan tentang apa yang dimaksud dengan matriks, jenis-jenis matriks, hitungan perkalian pada matriks, matriks identitas, invers matriks, determinan matriks serta contoh dari operasi matriks.
Semoga bagi kalian yang sedang membutuhkan artikel ini untuk sebagai syarat melengkapi tugas sekolah, kuliah bahkan untuk tugas akhir/ skripsi agar dapat bermanfaat. Berikut ini adalah penjelasannya.
Halo sahabat MB dimana pun anda berada, di bawah ini saya akan memaparkan tentang apa yang dimaksud dengan matriks, jenis-jenis matriks, hitungan perkalian pada matriks, matriks identitas, invers matriks, determinan matriks serta contoh dari operasi matriks.
Semoga bagi kalian yang sedang membutuhkan artikel ini untuk sebagai syarat melengkapi tugas sekolah, kuliah bahkan untuk tugas akhir/ skripsi agar dapat bermanfaat. Berikut ini adalah penjelasannya.
Yang dimaksud dengan matriks adalah sebuah susunan-susunan bilangan yang memiliki bentuk persegi panjang maupun yang mempunyai bentuk persegi dengan telah diatur dengan berdasarkan baris dan juga kolom. Akan tetapi selain itu pula ada juga yang sering menyebut matriks itu yakni susunan bilangan-bilangan dan terdiri atas baris dan kolom.
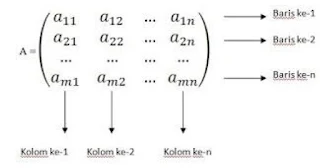
Dalam matriks, dengan pemberian sebuah nama maupun notasi matriks di haruskan menggunakan huruf besar (kapital) contoh, matriks A, matriks B, matriks C, matriks D, matriks E dan seterusnya. Maka dari itu, dibawah ini adalah notasi dari matriks yang terdiri dari 2 yakni sebagai berikut:
Dalam matriks, dengan pemberian sebuah nama maupun notasi matriks di haruskan menggunakan huruf besar (kapital) contoh, matriks A, matriks B, matriks C, matriks D, matriks E dan seterusnya. Maka dari itu, dibawah ini adalah notasi dari matriks yang terdiri dari 2 yakni sebagai berikut:
B. Jenis-jenis Matriks
Adapun jenis-jenis dari matriks terdapat tiga (3) macam yakni sebagai berikut:
1. Matriks baris,
Matriks baris adalah matriks yang jumlah baris lebih sedikit dari jumlah kolom
2. Matriks kolom
Matriks kolom adalah matriks yang jumlah baris lebih banyak dari jumlah kolom
3. Matriks persegi
Matriks persegi adalah matriks yang jumlah baris sama dengan jumlah kolom sehingga memiliki kesamaan jumlah. Berikut ini adalah contoh dari jenis-jenis matriks yang dapat anda lihat sebagai berikut :
C. Matriks Identitas
Matriks identitas sering di singkat dengan bentuk 'I' yang merupakan matriks persegi dimana dari semua elemen-elemennya nol, terkecuali pada diagonal utamanya.
D. Transpose Matriks
Pada tranpos matriks A ditulis dengan Aᵗ atau Aᴵ. Perhatikan gambar berikut:
Kemudian selain dari pada itu, didalam perkalian transpose matriks berlaku dengan rumus " Am.n maka Aᴵ n.m".
E. Determinan Matriks
Di dalam determinan matriks ini, jika determinan matriks A maka cara penulisannya adalah det A. Pada determinan matriks hanya terdapat jenis matriks persegi saja dan tidak akan ada jenis matriks lainnya, apabila sahabat Materi Belajar (MB) menemukan jenis soal matriks yang berodo satu (1), itu berarti hasil dari soal tersebut yakni angka itu sendiri dan apabila sahabat mendapatkan soal matriks yang berordo dua (2), maka sahabat dapat mengerjakannya dengan rumus det A = ad-bc
F. Menentukan Minor Matriks ordo 2
Di dalam minor matriks sangat sering dijumpai dengan singkatan "M". Contohnya sahabat MB mendapatkan soal matriks seperti matriks A = (a=1. b=3, c=-2, dan d=5) maka, sahabat MB dapat mengerjakan soal tersebut dengan cara seperti di bawah ini :
G. Menentukan Cofaktor Matriks ordo 2
Di dalam cofaktor matriks sangat sering dijumpai dengan singkatan "C". Apabila sahabat MB mempunyai soal matriks yang memiliki kesamaan seperti pada point F (minor matriks), maka sahabat MB dapat mengerjakan soal dari cofaktor matriks dengan cara seperti di bawah ini : Metode Pembelajaran Tentang Dasar Matriks
Pada tranpos matriks A ditulis dengan Aᵗ atau Aᴵ. Perhatikan gambar berikut:
E. Determinan Matriks
Di dalam determinan matriks ini, jika determinan matriks A maka cara penulisannya adalah det A. Pada determinan matriks hanya terdapat jenis matriks persegi saja dan tidak akan ada jenis matriks lainnya, apabila sahabat Materi Belajar (MB) menemukan jenis soal matriks yang berodo satu (1), itu berarti hasil dari soal tersebut yakni angka itu sendiri dan apabila sahabat mendapatkan soal matriks yang berordo dua (2), maka sahabat dapat mengerjakannya dengan rumus det A = ad-bc
F. Menentukan Minor Matriks ordo 2
Di dalam minor matriks sangat sering dijumpai dengan singkatan "M". Contohnya sahabat MB mendapatkan soal matriks seperti matriks A = (a=1. b=3, c=-2, dan d=5) maka, sahabat MB dapat mengerjakan soal tersebut dengan cara seperti di bawah ini :
Di dalam cofaktor matriks sangat sering dijumpai dengan singkatan "C". Apabila sahabat MB mempunyai soal matriks yang memiliki kesamaan seperti pada point F (minor matriks), maka sahabat MB dapat mengerjakan soal dari cofaktor matriks dengan cara seperti di bawah ini : Metode Pembelajaran Tentang Dasar Matriks
